Translating aspects of cognitive load theory into practice: nuanced results from the worked example effect in South African mathematics classrooms

Ashley Abbott, PhD Student and lifelong mathematics teacher, University of Oxford, UK

Introduction

Cognitive load theoryAbbreviated to CLT, the idea that working memory is limited ... More (CLTCognitive Load Theory - the idea that working memory is limi... More) needs little introduction for many teachers and schools, with a myriad of books being published especially for teachers on the subject (e.g. Garnett, 2020). However, the theory is not well integrated into the South African context, and there is a paucity of classroom-based CLT research not only within South Africa, but also more globally. This is exemplified by Ollerton et al. (2020, p. 36), who state that:

Most studies that contribute to CLT involve memorising novel ideas in short-term or laboratory contexts, seldom in authentic educational contexts over time and often with willing adult learners rather than, for example, unwilling adolescents.

This article seeks to bridge this gap between theory and classroom practice and expands the study by Abbott (2021), which found that female students and those of a low socioeconomic background in South Africa were significantly more likely to find worked examples beneficial for their learning when compared to male students and those from a high socioeconomic background. This study focuses solely on the responses from the students from a low socioeconomic background, who attended a state-funded rural school situated in an impoverished area of South Africa.

Context

South Africa is a country of many contrasts, the most notable of which is the educational disparity between the upper and lower social echelons – a legacy of the apartheid period. As stated in a report by Amnesty International, ‘South Africa has one of the most unequal school systems in the world.’ (2020, p. 7) The report goes on to list many challenges facing the education system in South Africa, including poor infrastructure and teacher content knowledge. Additionally, several studies have also found that mathematics teachers in South Africa often have poor mathematical content knowledge (Amnesty International, 2020; Bansilal et al., 2014; Venkat and Spaull, 2015). On an international scale, South Africa has also consistently ranked as one of the poorest-performing countries surveyed in the Trends in International Mathematics and Science Study (TIMSSTrends in International Mathematics and Science Study – a ... More) (Bowie et al., 2022; Mullis et al., 2016).

Cognitive load theory (CLT)

Since its inception in the 1980s (Sweller and Cooper, 1985), CLT has bloomed into a burgeoning topic of debate among educational researchers and teachers alike. In short, CLT is underpinned by the notion that we have a limited working memory capacity, and aims to balance the cognitive load of classroom resources that students must learn from. Emphasis is placed on the word balance to highlight the fact that the goal of CLT is not merely to reduce cognitive load, but rather to adapt it based on the level of knowledge of the student. 

It is a theory that has developed over time to now include 15 different cognitive load effects (Sweller et al., 2019). Seen to be one of the most widely studied effects, the worked example effect documents how studying worked examples leads to improved learning gains when compared to the more means–ends analysis of conventional problem-solving. The success of using worked examples has been widely cited in many topics within mathematics (Carroll, 1994; Paas, 1992; Paas and Merrienboer, 1994). Learning gains have also been experienced by students without direct instructionA method of instruction in which concepts or skills are taug... More from the teacher (Zhu and Simon, 1987). However, it is important to consider whether the conclusions from the worked-example research originate from laboratory (e.g. Paas, 1992; Paas and Merrienboer, 1994) or more naturalistic settings (e.g. Carroll, 1994; Zhu and Simon, 1987).

Given the plethora of studies on CLT, little is known about its effect on other groups of students, such as those of different genders and socioeconomic backgrounds. However, Bevilacqua (2017, p. 190) states that ‘[t]here is enough evidence in the literature to support the inclusionAn approach where a school aims to ensure that all children ... More of gender differences in cognitive load as a further upgrade to cognitive load theory’.

Method

Participants included 99 students (53 female and 46 male, aged 14–15 years) from a rural school in South Africa. The intervention comprised seven stages, as summarised in Figure 1. In Stage 5 of the intervention, students completed eight backwards-faded worked examples of increasing complexity. Backwards-faded worked examples allow for a scaffolded approach in the transition between studying full worked examples and structured practice: a series of examples are presented where the first is fully complete, the second example omits the last step, the third example omits the last and penultimate steps, with subsequent examples omitting increasingly more steps, until only the problem step remains. By doing so, students initially only need to focus on the missing steps of the calculations before they attempt to complete the full procedure.

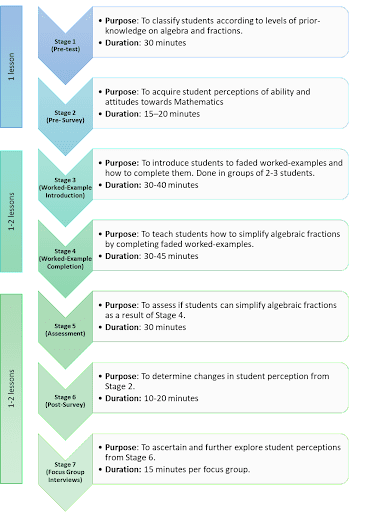
Figure 1: Research design and sequence

After completion of Stage 5, students completed a paper-based post-intervention survey to gauge their perceptions and attitudes towards mathematics after the intervention. However, the results discussed in this paper originate from Stages 6 and 7 of the intervention. Although the intervention was conducted in English, only six per cent of the student participants speak English at home, with 91 per cent instead speaking Xhosa. The language of instruction at the school was a blend of English and Xhosa.

The research questions guiding this report are:

1. How do students perceive the use of backwards-faded worked examples in the classroom? 
2. To what extent are gender differences evident in student perceptions of the usefulness of worked examples for their learning?

Results 

More female students (82 per cent) than males (64 per cent) felt that completing the backwards-faded worked examples helped them to simplify the algebraic fractions. These results are not statistically significant (χ2[1]=3.2; p=.07; phi=.19) and are highlighted in Figure 2.

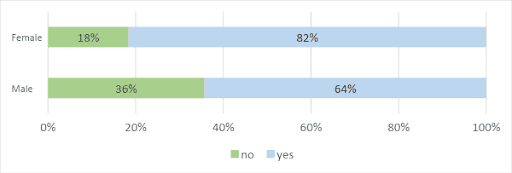
Figure 2: Results of student survey question asking ‘Did you find that completing the worked examples helped you understand how to do algebraic fractions?’

Results from the survey also indicate that 68 per cent of students perceived backwards-faded worked examples to be helpful and wanted them to be used more in class. When asked to elaborate on their reasons why, most of the students gave brief explanations, which have been organised into three themes: recall and learning, learning without help from a teacher or peer, and anxiety and ability. These are shown below, with indicative examples of student statements (students quotes are left grammatically unchanged).

Theme 1: Recall and learning

‘They helped understand and to remember other examples I once given before.’ (Student A)

‘The worked examples helped me to understand the steps of simplifying. I have something I know now in algebraic fractions.’ (Student B)

‘Yes, it made me completing the questions quite easy, And the worked-examples points or gives me a direction in which I can follow.’ (Student C)

‘Because I was confused I did not now what to do and the example helped me with my problems.’ (Student D)

Theme 2: Learning without the help of a teacher or peer

‘Yes because I can make maths by my own self and don’t need help to my friend.’ (Student E)

‘To algebraic fractions to how to do and if teacher don’t do a work example.’ (Student F)

‘They have helped me a lot and I can do at home.’ (Student G)

Theme 3: Anxiety and ability

‘Because I get very nervous and frustrated I even forget how to work problems. Sometimes the paper intimidates me when it is huge or a lot.’ (Student H)

‘Because I am weak.’ (Student J)

Discussion

A limitation is noted for this study in that the sample size is too small to generalise to a larger population. Thus, the results should be interpreted considering the context within which the study was conducted.

Research question 1

Most of the students’ comments related to some aspect of recall and learning in general (Theme 1), with Student A emphasising that the worked examples helped with recalling similar examples. Other students (B, C and D) provided statements that were in line with the general premise of the worked example effect, in that the studying of worked examples is beneficial for student learning under certain conditions. 

In accordance with the views expressed by Zhu and Simon (1987), some students indicated that the use of worked examples helped them to learn the mathematical content without the help of peers (Student E) or direct instruction from the teacher (Student F). Student G also indicated that the worked examples enabled him to complete the work at home, which is an interesting caveat to explore in the future with students who are not able to access help outside of the classroom.

Theme 3, surrounding anxiety and ability, provides an interesting avenue for deeper analysis, as the effects of worked examples on mathematics anxiety and perception of mathematical ability, or vice versa, have not yet been documented in detail. 

Research question 2

Although not significant, (χ2[1]=3.2; p=.07; phi=.19), the results from Figure 2 imply that female students may prefer the use of backwards-faded worked examples when compared with their male counterparts. This offers an important addition to the study by Abbott (2021), as these results come from a small sample of that research data. Although gender effects have not been widely cited within CLT research, it may prove to be an interesting and worthwhile caveat to explore, as suggested by Bevilacqua (2017).

Conclusion

Three themes relating to recall and learning, learning without help from a teacher or peer, and anxiety and ability emerged from the student explanations as to why they found worked examples useful for their learning. These results explore the more nuanced aspects of student perceptions of the worked example effect in CLT, and, although taken from a small sample of South African students from a rural school, provide an interesting avenue for exploring the applicability of CLT to the mathematics classroom. 

Classrooms are also a complex and fascinating research space within which to work, and we, as teachers and researchers, must refrain from providing broad generalisations and an overly simplistic view of extremely complex processes such as the functioning of our working memory. This is exemplified by Chen et al. (2021, p. 31), who state that ‘mathematics teachers are often expected to work in limited ways using simplified and sometimes spurious or inappropriate, interpretations of Cognitive Load Theory (CLT) as justification’. As teachers, we are naturally attracted to new and exciting theories in education, and we must ensure that we understand what they can offer against the background of their limitations.