How can we apply Rosenshine’s principles in primary mathematics?

In 2012, Barack Rosenshine published the Principles of Instruction: a set of 10 research-based principles of instruction, along with suggestions for classroom practice. The principles come from three sources: (a) research in cognitive scienceThe study of the human mind, such as the processes of though... More, (b) research on master teachers, and (c) research on cognitive supports.

The 10 Principles of Instruction are as follows:

• Principle 1: Begin a lesson with a short review of previous learning: Daily review can strengthen previous learning and can lead to fluent recall.
• Principle 2. Present new material in small steps with student practice after each step. Only present small amounts of new material at any time, and then assist students as they practice this material.
• Principle 3. Ask a large number of questions and check the responses of all students: Questions help students practice new information and connect new material to their prior learning.
• Principle 4. Provide models: Providing students with models and worked examples can help them learn to solve problems faster.
• Principle 5. Guide student practice: Successful teachers spend more time guiding students’ practice of new material.
• Principle 6. Check for student understanding: Checking for student understanding at each point can help students learn the material with fewer errors.
• Principle 7. Obtain a high success rate: It is important for students to achieve a high success rate during classroom instruction.
• Principle 8. Provide scaffolds for difficult tasks: The teacher provides students with
  temporary supports and scaffolds to assist them when they learn difficult tasks.
• Principle 9. Require and monitor independent practice: Students need extensive, successful, independent practice in order for skills and knowledge to become automatic.
• Principle 10. Engage students in weekly and monthly review: Students need to be involved in extensive practice in order to develop well-connected and automatic knowledge.

In this post, Jess Mahdavi-Gladwell, Chartered Teacher, explores their application in primary maths.

This content was originally produced as part of the Accelerate programme, a Department for Education-funded early career teacher programme designed and delivered by Education Development Trust with the Chartered College of Teaching. It is used here with kind permission of Education Development Trust.

Rosenshine (2012) presents 10 evidence-informed principles of instruction for teachers to use in understanding, learning and honing their classroom practice. This blog will focus on how the principles can be utilised in a meaningful and practical way to support pedagogy (without increasing workload or demands on time).

Within the area of maths teaching and learning in the primary age range, there has been a shift from focussing on and valuing procedural fluency (speedy and accurate calculations) to supporting conceptual understanding. This simply means that rather than focussing on multiplication as a formal written method we think of the concept of multiplication as something which supports children when they calculate mentally, when they learn about division, when they learn about fractions and many more complicated concepts within and beyond the primary years.

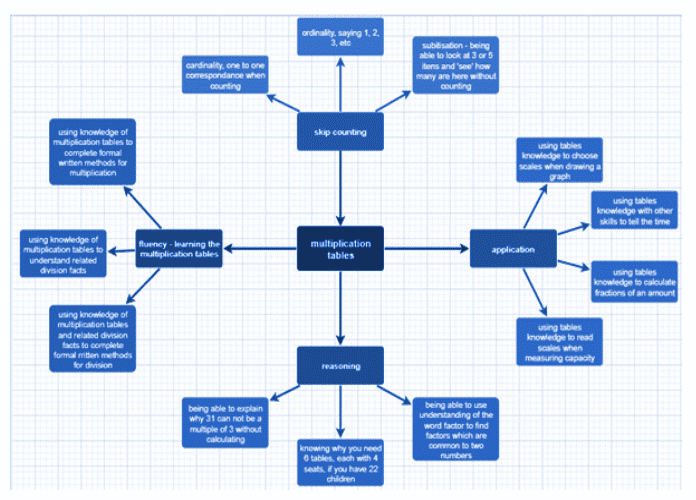
The concept map, below, shows an example of how we could illustrate the understanding of multiplication and how that relates to mathematical learning within the wider primary curriculum.

Principle 2: Present new information in small steps and have children practice after each step is introduced

If we begin by looking at the second principle, ‘Present new material in small steps with student practise after each step’, teaching for mastery and the idea that pupils will acquire (and continue to acquire) a deep, long-term, secure and adaptable understanding of mathematical concepts, fits well with this.

Many schools are using schemes and resources such as White Rose Maths, Power Maths, Maths No Problem to embed and develop this kind of teaching in our classrooms. Schemes such as these can provide, for example, a yearly overview to suggest the order in which different areas of maths should be covered and the length of time that should be spent on each subject.

Coverage is often broken into small steps with examples of activities to support the development of fluency and reasoning. Some schemes also include textbooks and/or workbooks and online materials which can, arguably, reduce teacher workload in relation to planning and compensate for developing subject knowledge.

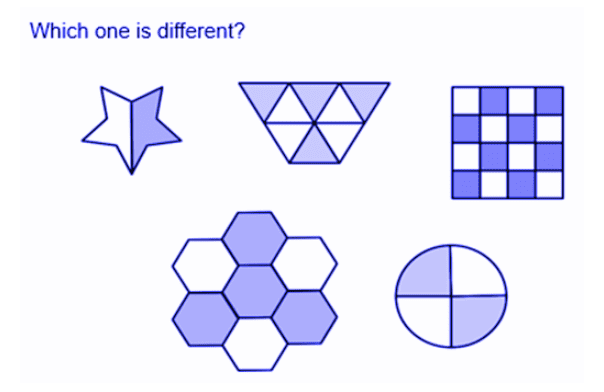
The use of variation as part of intelligent practise can further develop this idea of small steps teaching and learning. Variation can be conceptual or procedural: conceptual variation revolves around using a variety of representations for each concept (e.g. showing fractions of circles, pentagons, bars, amounts) so that children don’t have a misconception that fractions only relate to ‘pizza slices’ for example. The example below illustrates this conceptual variation.

(Image reproduced with permission of Third Space Learning.)

Procedural variation is more aligned with the idea of small-step learning, using carefully considered and precisely ordered calculations to aid the understanding of relationships. For example, if we look at these groups of calculations and how relationships and patterns can support understanding of concepts.

Additionally, the use of the Concrete, Pictorial, Abstract approach, discussed in more detail below, supports this idea of valuing conceptual understanding as well as procedural fluency.

Principle 4: Provide models

Providing modelling is usually a key aspect of small step teaching, for example  when schools follow the Shanghai approach, often you would see a prepared example shown on the IWB along with a flip chart on either side showing further modelled examples.

There is a move away from listing procedural steps (although this has value when a method or procedure is being taught) and a focus on embedding conceptual understanding.

An example of this could be the activity shown in the image below. A fraction wall is used in conjunction with a number line and unit fractions are marked accurately on the number line.  The teacher models how to complete the first part of the task on the flip chart before allowing the children to work independently, with a partner or with adult support to place more unit fractions on the number line accurately, using the provided scaffold of an accurate and aligned fraction wall.

This activity will allow children to observe and notice that when comparing unit fractions, a larger denominator means a smaller fraction.

In my opinion, this is an effective way for children to learn about comparing and ordering unit fractions. It supports their understanding of why the unit fractions are ordered thus.

An alternative way of teaching children to order fractions would be to teach two rules.

1. When the numerator is the same, the bigger the denominator, the smaller the fraction
2. When the denominator is the same, the bigger the numerator, the bigger the fraction

Principle 6: Check for student understanding

After effective modelling, it is vital that we check that pupils understand what has been taught. This is commonly known as AfLAssessment for Learning (also known as formative assessment)... More (Assessment for LearningKnown as AfL for short, and also known as formative assessme... More) and links well with principle 3: ask a large number of questions to check responses of all students.

This can include practices such as use of mini whiteboards for all children to give responses, and alternate questioning for each partner in a pair (this allows us to see independent application of a task where there is partner support of understanding).

Requiring a response from most or all pupils minimises the potential for children to opt-out of responding (and possibly listening).

Other possible techniques include:

• requiring all pupils to listen to a response and decide whether to support or challenge;
• spoof assessment (where pupils find and explain mistakes);
• asking children to physically move or point to one of a choice of answers.

Choral responses can reduce anxiety and allow children to learn and respond without being the focus of uncomfortable attention.

Throughout questioning, there will also be modelling of appropriate responses to ‘wrong’ answers which should also support children to feel able to respond and take risks in learning.

This type of involvement allows for the teacher to spot and address misconceptions before moving to guided practice (practice within lesson, under the support and supervision of the teacher).

Principle 8: Provide scaffolds for difficult tasks

Within the lesson, as part of guided practise and during independent recording, the teacher provides students with temporary supports and scaffolds to assist them when they learn difficult tasks. In class differentiation by task has not been shown to impact positively on pupil outcomes. Hattie (2009) found the effect of differentiation to be among the weakest.

When we give lower-attaining children less challenging work and, in some cases, deny them access to the curriculum we are supposed to be teaching them, we simply widen the attainment gap.

By giving higher-attaining children new learning as soon as they have shown procedural capability, we are showing them that they don’t need to think independently, that we as teachers, don’t expect them to struggle, and we run the risk of creating children who do not know how to think around a problem and apply what they know independently in novel situations.

The CPA approach supports this, we begin by undertaking tasks using apparatus. For example, when introducing the concept of addition as a mathematical concept in EYFS, we would begin by looking at a concrete example which would be familiar to the children. I have two slices of mango and then my sister gives me one more, how many slices of mango do I have now.

This learning could be acted out with real or pretend food items, books, toys or other items within a familiar environment. Children are linking something they understand (having and being given items) with something novel (the mathematical symbol for addition +). As children become more confident at using the language to describe the concept of adding more, we can move to showing (or drawing) images of the items being added before eventually moving to the abstract stage of completing a calculation.

This image, for example, could be used to support calculation of 6 + 1 = (There are 6 apples on the tree and one on the floor, how many apples altogether?) or 7 – 1 = (There were 7 apples on the tree, one fell off, how many apples are left?). Children could learn to draw images for themselves to support simple calculations or word problems.

Similar calculations could be completed with the support of concrete apparatus, toy apples or cubes for younger children or children at an earlier stage of understanding. As children gain confidence and build understanding and fluency, the same picture could be used to support understanding of 7 = __ + 6 (There are 7 apples in total, there are 6 on the tree, how many are on the floor?) or 1 + __ = 7 (One apple is on the floor, if there are 7 apples altogether, how many are on the tree?).

This use of concrete apparatus can, and should, be used throughout the primary phase (and beyond, but that’s a separate matter), for example:

• Base ten equipment (or dienes) can allow children who struggle to retain addition facts such as number bonds to ten, but who understand the concept of addition to access more complicated calculations. This allows them to develop understanding while supporting them to continue to rehearse areas where more practise is needed.
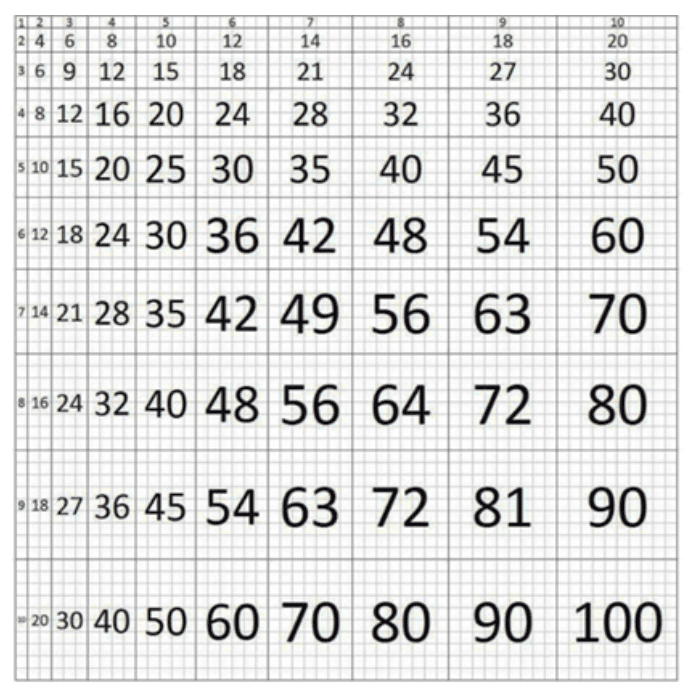
• Use of multiplication grids, for example, or multiple lists when learning formal written methods or when learning fractions so that what we are assessing is the new learning and understanding of that rather than the ability to recall multiplication facts.

The use of the conceptual grid (below) allows for practise while reinforcing the concept of multiplication. The pupils can see the calculation and answer pictorially (7 in a row x 2 rows = 14). This can also be used to allow children to notice, for example, that square numbers are indeed square. Once this concept is understood, there is no need for children to learn square numbers arbitrarily as a list.

Choice of concrete apparatus and pictorial support is key, the example above providing much more effective support for learning than a simple list or grid which does not reference the concept of multiplication.

All of these principles, together, lead to achieving principle 7: obtain a high success rate, reinforcing achievement.

So how does it work in reality? The ten principles, although clear and evidence based, can seem overwhelming when thinking about including them all in a lesson.

It is important to remember that, while I would suggest you bear them in mind when planning a series of lessons, the aim of sharing an understanding of these principles with a focus on primary maths does not indicate that every principle needs to be addressed in every hour-long unit of teaching and learning time.

It is important to acknowledge that, as an early career teacher, you will most likely be given guidelines within which you are expected to work. You will be given a scheme or learning or curriculum map to follow. Hopefully you will be given clearly explained expectations about any school-agreed format for maths lessons. There may be certain resources, textbooks and other materials that you are asked or directed to use.

Within this guidance, there will also be space for you to be authentic, to do what you believe in, to learn and develop yourself as an educator.

References

Rosenshine B (2012) Principles of Instruction: Research-Based Strategies That All Teachers Should Know. American Educator  36(1): 12 – 39. Available at: https://www.aft.org/sites/default/files/periodicals/Rosenshine.pdf (accessed 16 December 2020).

Marshal M, Clark D and Carey M (2015) The use of Mathematical Investigations in a Queensland Primary School and Implications for Professional Development. International Journal for Mathematics Teaching and Learning: 1-20.

View the Principles of Instruction research paper

Return to the Principles of Instruction collection