A curriculum masterclass: Inspired by lessons we have learned from mathematics

Rebekah Gear, Hillocks Primary Academy, Sutton-in-Ashfield, UK

The Teaching for Mastery ‘Five Big Ideas’ encompass the pedagogical reform underpinning the primary maths curriculum, implemented across English primary settings in 2014 (Boylan et al., 2019; NCEMT, 2017). It was brought about to improve mathematical achievement for all, heavily influenced by best practices in Shanghai and Singapore (Blausten et al., 2020). It was heralded as an approach that promotes coherence within the maths curriculum at a time when Wiliam (2013) was considering what forms the pillars of the careful construct of curriculum design. It is no surprise that mathematics has long been held on the primary curriculum pedestal. This article reflects on the head start that the primary maths curriculum has had in understanding what effective curriculum design looks like in practice. It will unpick how these Five Big Ideas (Figure 1) form the foundations of a potential curriculum masterclass, inspired by what we have learned about teaching and learning in maths and underpinned by the notion of teaching for mastery – the belief that every child can succeed (Boylan et al., 2019).

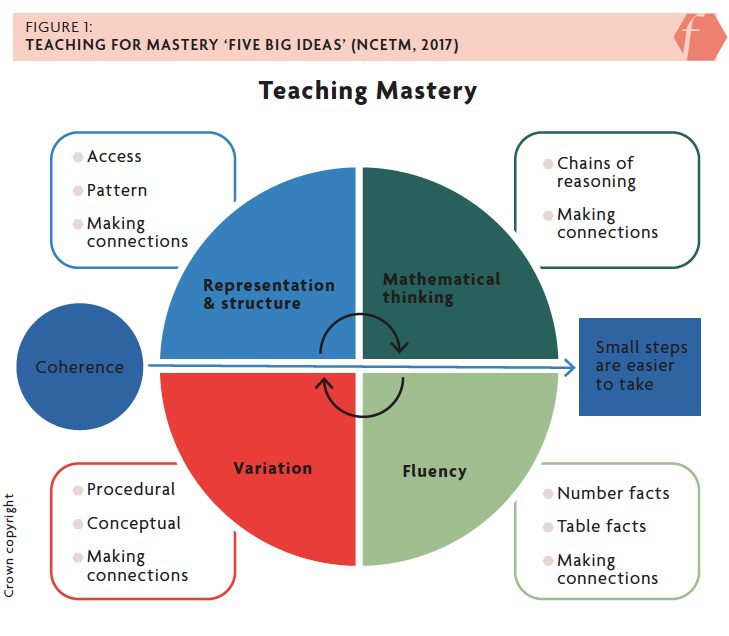
The first idea is fluency. We must begin by understanding that fluency encompasses so much more than simply memorising ‘facts’. Cockcroft (1982) highlighted the risk that simple rote-rehearsing these facts poses, leaving them essentially isolated or arbitrary when and if not connected to a conceptual structure. This is often coupled with the misconception that mastery is about rote learning or repeated practice. If we are superficial here with our understanding of fluency, we could easily merge it with mechanical performance; however, Cockcroft (1982) determines a difference between the two (p. 70):

Fluent performance is based on an understanding of the routine which is being carried out; mechanical performance is a performance by rote in which the necessary understanding is not present.’

However, there is a place for quick, efficient recall of key declarative knowledge, in terms of how it supports children to overcome cognitive load. There is certainly a lesson to be learned by each subject in ensuring that it understands what principle pieces of knowledge children need to have mastered to enable them to succeed in subsequent experiences of that subject year on year.

However, fluency is also about demanding flexibility. This flexibility is what enables children to transition between different contexts and representations, to recognise relationships and make connections, and to make appropriate choices from a whole toolkit of methods, strategies and approaches, wandering into the realms of reasoning (Hasanah et al., 2019).

This flexibility is often tested year on year in other subject disciplines and seems to sit nicely in the realms of Wiliam’s (2013) notion of vertical integration. We must ensure that not only do we know what knowledge children are going to need, but we must also be mindful of how each subject creates curriculum stories across the whole school, which enables children to work flexibly and fluently in their learning.

The next idea is the complex matter of variation. Central to the idea of teaching with variation is ensuring that the essential feature is highlighted. Watson and Mason (2006) cite variation as a powerful teaching and learning strategy. This is the consequence of how it evokes children’s understanding of mathematical structures, encouraging them to both engage with and think critically about what they notice. It can be both exhausting and exciting, as, by changing the non-essential features, children begin to explore the similarities and differences. This may come to life in how something is represented using different apparatus (an example of conceptual variation) or within questions that are offered to pupils (procedural variation).

Whichever strand you explore, it is important to recognise that the route of this is knowing our curriculum’s concepts. Myatt (2020) talks about how understanding these concepts (or ‘big ideas’, as she also refers to them) brings coherence to our curricular thinking. So, not only do we need to have a clear understanding as to what these concepts are, but we must also begin to understand how to use variation to highlight the essential features of a concept through varying the non-essential features. Consider this: how do you take the same ‘big idea’ and apply it to a different problem? For example, how do children take their understanding of the ‘concept’ of civilisations and apply this time and time again to different historical studies?

The key here, in line with what Wiliam (2013) declares as good curriculum design, is ensuring that it is appropriate, and that learning experiences are continuously built upon, and not simply repeated.

This leadings onto representation and structure. In terms of maths, we tend to think about the Singaporean approach: concrete, pictorial and abstract, influenced by Bruner’s enactive and symbolic methods of representation (Bruner, 1966). However, there is something to be considered here in how representations are required to give clarity and thus expose the structure of the concept being taught (Boyd and Ash, 2018). There will also be, across all subjects, key representations that children will meet time and time again. It is certainly worth considering, whether through practical materials, diagrams or even subject-specific stem sentences.

There is further evidence that suggests how using different representations, particularly concrete materials, creates a level-learning playing field. It has been observed in the Early Years that when children are posed with problems to solve using mathematical manipulatives, very little disparities are witnessed; it is when the ‘talking’ begins that what then appears to be a gap in understanding is unearthed (McCray et al., 2019). The ongoing challenges of this vocabulary ‘gap’ is something with which we are not unfamiliar, and neither is it unique to mathematics. However, in terms of combatting it, I think that we need to think carefully as to how we provide resources or representations that foster ‘equitable’ opportunities for all children to grasp and understand new learning and concepts.

Next, we come to think about how we evoke children’s thinking, both encouraging and enabling children to think ‘mathematically’ or ‘geographically’ and so on. It demands the deepest levels of cognition and sits within the realms of reasoning and problem-solving. This has potentially perpetuated some misconceptions linked to its presentation, and, in the context of mathematics, there has been a risk that the application of mathematical thinking and reasoning is there to develop a child’s mathematical explanations (Hunter, 2017). This has often translated in practice into something formulated in isolation, depicted simply by recorded words or images. Instead, it should be situated as a co-dependent cognitive experience that is developed through rich opportunities to collaborate, converse and critically evaluate the complexities of the problem-solving process, in partnership with peers. Vygotsky advocated learning as a social experience, suggesting that small groups and pupil dialogues should underpin learning in the classroom (Smagorinsky, 2007). We need to ensure that all curriculum experiences support this and that we provide children with the correct support to interrogate their thinking when learning and exploring new content, which is both a mysterious and sometimes messy experience.

Finally, we come to coherence or the small steps. This is spoken about explicitly by Wiliam (2013) in terms of keeping a curriculum focused, and thus manageable, while also ensuring that it is coherent, building upon what students have learned before but not forgetting what comes next. Schmidt et al. (2005) previously synthesised this notion, stating that successful curricula illustrate the importance of detail, sequencing and alignment of content, so it is worth giving both careful consideration and time.

Herein concludes why I believe that the mathematics curriculum has had both a slight and a subtle head start in mastering a curriculum design. I believe that it continues to be rigorous and ambitious in how it creates opportunities for children to connect new knowledge, through exploratory and exciting experiences and, most importantly, founded on inclusive practice, underpinned by the Teaching for Mastery ‘Five Big Ideas’ and thus the belief that every child can succeed (Boylan et al., 2019). Although these principles have mostly been situated within the maths curriculum, I am sure that some crossover in other curriculum subjects has been evoked along the way. I believe that these are neither unique nor situated only specifically within maths; instead, they can be easily applied across our curriculum with due care, attention and reflection.