Navigating the mathematics curriculum in England from Year 7 to GCSE

As a teacher of mathematics, I heard many conversations about whether GCSE is a two- or three-year programme of study and in what order we should teach the various interconnected topics in mathematics. I agree that the second question deserved much consideration and deliberation but could never understand the first point. My belief is that the GCSE mathematics programme of study starts in Reception. Consequently, my teaching needed to build on the prior learning in primary.
I entered our profession in 2001 to teach mathematics because I believe that learning mathematics develops habits of mind (Cuoco et al., 1996) that are essential to success in all aspects of life. In a single word, mathematics develops ‘thinkers’. As a secondary teacher, I was accountable for GCSE results and maximising take-up of mathematics post-16.
In order to plan the delivery of the required GCSE mathematics curriculum, I felt that I needed to answer these two questions:
- How does the GCSE content fit with and build on the mathematics that each child learns from Reception?
- How do I ensure that I am developing thinkers with mathematical habits of mind and not just the ability to get a grade at GCSE?
How does the GCSE content fit with and build on the mathematics that each child learns from Reception?
This extract from the DfEDepartment for Education - a ministerial department responsi... More GCSE specification (DfE 2013a, p. 3) identifies the need to consider Key Stage 3 (DfE 2013b) learning. I also believe that Key Stage 1 and Key Stage 2 should be considered by a secondary school teacher of mathematics.
This document sets out the learning outcomes and content coverage required for GCSE specifications in mathematics. In subjects such as mathematics, where topics are taught in progressively greater depth over the course of key stage 3 and key stage 4, GCSE outcomes may reflect or build upon subject content which is typically taught at key stage 3.
Consequently, a scheme of work is needed that starts in Year 7, builds on the previous years and provides the opportunity for every child to access the full specification, whilst knowing that some children will enter the foundation level of GCSE. Although there is a prescribed National Curriculum in England, there is no prescribed national scheme of work (learning). The National Centre of Excellence in the Teaching of Mathematics (NCETM) discusses ‘mathematical habits of mind’ and suggests progression maps within the domains of: the structure of the number system; operating on number; proportional reasoning; sequences and graphs; statistics and probability; and geometrical reasoning. The NCETM also recommends that mathematics lessons should have coherence, which they describe as:
Connecting new ideas to concepts that have already been understood, and ensuring that, once understood and mastered, new ideas are used again in next steps of learning, all steps being small steps.
Considering the statement ‘apply and interpret limits of accuracy, including upper and lower bounds’ (DfE, 2012a, p. 5) from the GCSE specification for number, how does this fit with the prior learning? What are the connected steps? Where do I find a scheme of work that provides a coherent pathway? I believe that my priority is designing well-crafted lessons and not a scheme of work.
Matt Nixon and Steve Lomax, the creators of Kangaroomaths.com (2018), developed a scheme of work (SOW) from Reception to Year 11, which now has an interactive interface through MathsNav.com. This scheme of work is in the public domain and is free of charge. The big picture underpinning the SOW identifies how each topic builds on previous topics. As an example, Table 1 identifies the build up to ‘apply and interpret limits of accuracy, including lower and upper bound’. For the majority of students, a stage relates to a school year.
| Stage | Content/topic |
| Stage 10 | Apply and interpret limits of accuracy, including upper and lower bounds. |
| Stage 9 | Use inequality notation to specify simple error intervals due to truncation or rounding. Apply and interpret limits of accuracy. |
| Stage 8 | Round numbers and measures to an appropriate degree of accuracy (e.g. to a specified number of decimal places or given number of significant figures). |
| Stage 7 | Round numbers and measures to an appropriate degree of accuracy (e.g. to a specified number of decimal places or one significant figure). |
| Stage 6 | Round any whole number to a required degree of accuracy. |
| Stage 5 | Round any number up to 1,000,000 to the nearest 10, 100, 1,000, 10,000 or 100,000. |
| Stage 4 | Order and compare numbers beyond 1,000. Round any number to the nearest multiple of 10, 100 or 1,000. |
| Stage 3 | Compare and order numbers up to 1,000. |
| Stage 2 | Compare and order numbers from 0 up to 100. Use <, > and = signs. |
| Stage 1 | Identify and represent numbers using objects and pictorial representations, including the number line, and using the language of equal to, more than, less than (fewer), most and least. |
Table 1: Progression map for GCSE subject objective ‘apply and interpret limits of accuracy, including lower and upper bound’
Through MathsNav.com (2018; see Figure 1), I had a scheme of work that was calendared. The decision I needed to make in Year 7 was what stage should be chosen to teach to. This was dependent upon the prior attainment of the students in the class being taught. The overwhelming majority of children will start at Stage 7, but since mathematics is hierarchical, those not yet secure on earlier stages may need to start on either Stage 5 or Stage 6. Since there are still five years of learning, this does not preclude children from closing the gap. By the end of Stage 10, the content of the foundation tier has been covered.

How do I ensure that I am developing thinkers with mathematical habits of mind and not just the ability to get a grade at GCSE?
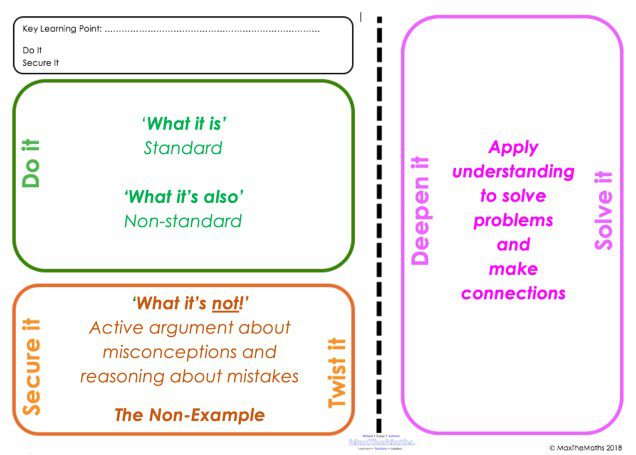
Having a coherent scheme to navigate my way through the curriculum, I then needed a lesson structure that supported the teaching for mastery approach recommended by NCETM. I am indebted to Steve Lomax (@MaxTheMaths, 2019) for his suggested lesson design (see Figure 2; Lomax and Bowman, 2018; Lomax, 2019), which he has agreed for me to include here.
The design embraces the core principles of variation theory by supporting teachers to carefully craft examples and exercises to secure and deepen pupils’ understanding of mathematical ideas by highlighting essential features of a concept through the use of:
- ‘what it is’ (standard)
- ‘what it is also’ (non-standard)
- ‘what it is not’ (non-examples)
- ‘applying understanding to solve familiar and unfamiliar problems’.
Consideration of how to craft the content along these lines is beyond the scope of this article.
With the framework of a coherent scheme of work and a suggested lesson design, I was able to focus my time on crafting lessons for the specific needs of the children I taught. I needed to consider how to teach the new content and then have the right choice of examples and exercises. I was able to concentrate on developing thinkers with mathematical habits of mind. The GCSE grade and enthusiasm to study mathematics post-16 followed as a consequence of my continual focus on learning and making connections with what has been learnt. Evidence of the positive impact is in this testimonial written by a Year 11 student:
Thank you so much for all you have done to teach and encourage me. Thank you for showing me there is a point and most importantly that I can do it. I have really enjoyed doing maths this year and can’t wait to be doing more next year! I never thought I would be saying this after my GCSE exams but it is true, and I can’t thank you enough for changing my view and making me believe in myself.
References
Cuoco A, Goldenburg E and Mark J (1996) Habits of mind: An organizing principle for mathematics curriculum. Journal of Mathematical Behaviour 15(15): 375–402.
DfE (2013a) GCSE mathematics: Subject content and assessment objectives for GCSE in mathematics. Available at: https://www.gov.uk/government/publications/gcse-mathematics-subject-content-and-assessment-objectives (accessed 21 February 2019).
DfE (2013b) Mathematics programmes of study: Key Stage 3. National Curriculum in England. Available at: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/239058/SECONDARY_national_curriculum_-_Mathematics.pdf (accessed 21 February 2019).
DfE(2013c) Mathematics Programmes of Study: Key Stage 1 and 2. Available at https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/335158/PRIMARY_national_curriculum_-_Mathematics_220714.pdf (accessed 28 March 2019)
KangarooMaths.com (2018) Key Stage ¾: Schemes of work for the 2014 curriculum. Available at: http://www.kangaroomaths.com/kenny2.php?page=Kschemeks3 (accessed 21 February 2019).
Lomax S (2019) Do it, twist it, solve it: Teaching for mastery. Available at: https://candomaths.org/blog/post/doit-twistit-solveit-teaching-for-mastery (accessed 21 February 2019).
Lomax S and Bowman D (2018) Challenge as an element of mathematics lessons. Available at: https://candomaths.org/blog/post/challenge-as-an-element-of-mathematics-lessons (accessed 21 February 2019).
MathsNav.com (2018) Secondary mathematics medium term plan 2018/19. Available at: http://mathsnav.com/ks3.html (accessed 21 February 2019).
NCETM (2017) Five Big Ideas in Teaching for Mastery. Available at: https://www.ncetm.org.uk/resources/50042 (Accessed 29 March 2019).










